The Young equation: relationship between material properties and contact angle
In the static case with contact angle ΘC, there is a vectorial equilibrium between surface energy of the solid σS, surface tension of the liquid σL and the solid-liquid interfacial energy σSL (see Figure 2). This equilibrium is expressed in the Young equation:
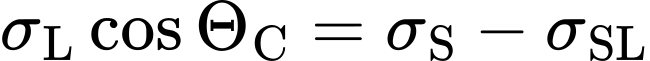
Where:
- σL: surface tension of the liquid
- θC: equilibrium contact angle
- σS: surface energy of the solid
- σSL: interfacial energy between liquid and solid
The surface energy of the solid and the interfacial energy between solid and liquid are usually unknown. However, if the contact angle of several test liquids on a solid surface is measured, the surface energy of the solid can be determined with the help of interaction models (see: Determining surface energy). In addition, further investigations of the work of adhesion are possible.
Contact angles provide information about wetting properties of the solid surface
Measuring the contact angle of a liquid on a solid provides information about the wetting behaviour of this combination. The desired wetting behaviour depends on the particular application.
With a contact angle of 0°, the droplet is completely spread on the solid surface. The drop forms a thin, sometimes monomolecular liquid film on the solid surface. This case is called complete wetting. With a contact angle of 180°, the drop lies spherically contracted on the surface and touches the solid only at one point. This case is called complete dewetting.
In practice, the contact angle usually lies between these two extreme values. Solid surfaces on which a contact angle ΘC of less than 90° is formed are generally described as having good wettability. Higher contact angles indicate that a surface is hardly wettable or not wettable at all.
One of the most vivid examples of particularly high contact angles can be found in nature: water droplets roll off the leaves of the lotus plant. No wetting takes place and the contact angle is correspondingly high. Because the beading drops transport dirt particles away, the leaves possess a self-cleaning effect. Today, attempts are being made to emulate this lotus effect in many technical areas: self-cleaning facades, ceramics and window glass are examples of such technical developments. Contact angle measurement is indispensable in the development of such products.
Contact angle measurements are the basis of many standards and norms that describe wetting characteristics. A substantial list of standards can be found here.
Application examples for contact angle measurements
Contact angle measurements are always useful when solids and liquids meet and when wetting and adhesion properties need to be controlled or modified. The fields of application are accordingly diverse. Important examples are:
- Surface coatings: Measurement of the contact angle on coated materials to evaluate the quality and uniformity of the coating.
- Painting and printing industry: Evaluation of the wettability of paints, varnishes and printing inks on various substrates.
- Textile industry: Determination of the wettability of textile fibres to check the quality of textile treatments, such as impregnation or dewatering.
- Medical devices: Characterisation of the wettability of medical implants to assess their biocompatibility.
- Food industry: Evaluation of the wettability of packaging materials to ensure printability and improve storage properties.
- Semiconductor industry: control of wettability on surfaces of semiconductor chips and substrates for microchip manufacturing.
- Environmental science: measuring the contact angle on leaf surfaces of plants to study self-cleaning effects and water distribution.
- Nanotechnology: Characterising the wettability of nanomaterials and nanoparticles to optimise their properties in various applications.
- Oil and gas industry: Assessing the wettability of rock surfaces to better understand the behaviour of oil and gas reservoirs.
- Cleaning and degreasing processes: Evaluating the efficiency of cleaning and degreasing agents on different surfaces to optimise effectiveness.