Ein Flüssigkeitstropfen bildet auf einer Festkörperoberfläche den Kontaktwinkel Θ aus. Der Kontaktwinkel ist anhängig von der Oberflächenenergie des Festkörpers, der fest-flüssig-Grenzflächenenergie, sowie der Oberflächenspannung der Flüssigkeit. Dieser Zusammenhang lässt sich durch die Young-Gleichung ausdrücken. Kontaktwinkelmessungen geben Aufschluss über das Benetzungsverhalten einer Flüssigkeit auf einem Festkörper.

Der Kontaktwinkel an der Drei-Phasen-Kontaktlinie

Um die Situation an der Grenzfläche zwischen verschiedenen Materialien näher zu beschreiben, ist der Kontaktwinkel Θ eine der wichtigsten Messgrößen. Der Kontaktwinkel kann gemessen werden, indem ein Flüssigkeitstropfen auf einer Festkörperoberfläche abgesetzt wird. Nun treffen drei verschiedene Phasen - Festkörper, Flüssigkeit und Gas - an der Drei-Phasen-Kontaktlinie aufeinander.

Ist das System in Ruhe, herrscht an der Drei-Phasen-Kontaktlinie ein Gleichgewicht der tangentialen Kräfte. In diesem Zustand bildet sich an der Drei-Phasen-Kontaktlinie der statische Kontaktwinkel Θ_C aus. Ist das System in Bewegung, etwa, wenn die Festkörperoberfläche gekippt wird, kann man die dynamischen Kontaktwinkel Θ_Adv und Θ_Rec bestimmen.

Messungen des Kontaktwinkels lassen sich mit Kontaktwinkelmessgeräten, wie die der OCA-Serie des Herstellers DataPhysics Instruments, durchführen. Erwähnenswert ist hierbei die Vielzahl an Zusatzmodulen, die Untersuchungen für verschiedenste Anwendungsfälle ermöglichen. Dazu gehören Nano- und Pikoliter-Dosiereinheiten für besonders kleine Tropfen, Thermostatisiereinrichtungen für Untersuchungen im Temperaturbereich zwischen −30 °C und 1800 °C sowie Feuchtegeneratoren zur Kontrolle der Luftfeuchtigkeit in der Messkammer.

Die Young-Gleichung: Zusammenhang zwischen Materialeigenschaften und Kontaktwinkel

Im statischen Fall mit dem Kontaktwinkel Θ_C herrscht ein vektorielles Gleichgewicht zwischen Oberflächenenergie des Festkörpers σ_S, Oberflächenspannung der Flüssigkeit σ_L und der fest-flüssig Grenzflächenenergie σ_SL vor (vgl. Abbildung 2). Dieses Gleichgewicht kommt in der Young-Gleichung zum Ausdruck:

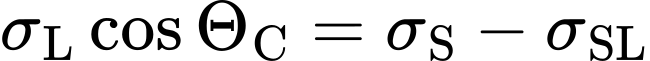
Wobei:

• σ_L: Oberflächenspannung der Testflüssigkeit
• θ_C: Kontaktwinkel im Gleichgewicht
• σ_S: Oberflächenenergie des Festkörpers
• σ_SL: Grenzflächenenergie zwischen Flüssigkeit und Festkörper

Die Oberflächenenergie des Festkörpers und die Grenzflächenenergie zwischen Festkörper und Flüssigkeit sind in der Regel unbekannt. Misst man allerdings den Kontaktwinkel mehrerer Testflüssigkeiten auf einer Festkörperoberfläche, lässt sich die Oberflächenenergie des Festkörpers mit Hilfe von Modellen bestimmen (siehe: Oberflächenenergie bestimmen). Außerdem sind weitere Untersuchungen der Adhäsionsarbeit möglich.

Kontaktwinkel geben Aufschluss über Benetzung des Festkörpers

Die Messung des Kontaktwinkels einer Flüssigkeit auf einem Festkörper gibt Aufschluss über das Benetzungsverhalten dieser Kombination. Das angestrebte Benetzungsverhalten ist von dem jeweiligen Anwendungsfall abhängig.

Bei einem Kontaktwinkel von 0° ist der Tropfen vollständig auf der Festkörperoberfläche ausgebreitet oder gespreitet. Der Tropfen bildet einen dünnen, manchmal monomolekularen Flüssigkeitsfilm auf der festen Oberfläche. In diesem Fall spricht man von vollständiger Benetzung. Bei einem Kontaktwinkel von 180° liegt der Tropfen kugelförmig zusammengezogen auf der Oberfläche auf und berührt den Festkörper nur an einem Punkt. In diesem Fall spricht man von vollständiger Entnetzung.

In der Praxis liegt der Kontaktwinkel meist zwischen diesen beiden Extremwerten. Festkörperoberflächen, auf denen sich ein Kontaktwinkel Θ_C kleiner als 90° ausbildetet, werden gemeinhin als gut benetzbar beschrieben. Höhere Kontaktwinkel deuten darauf hin, dass eine Oberfläche kaum oder gar nicht benetzbar ist.

Eines der anschaulichsten Beispiele für besonders hohe Kontaktwinkel finden wir in der Natur: Auf den Blättern der Lotospflanze perlen Wassertropfen ab. Es findet keine Benetzung statt und der Kontaktwinkel ist entsprechend hoch. Weil die abperlenden Tropfen Schmutzpartikel abtransportieren, kommt es zu einem Selbstreinigungseffekt der Blätter. In vielen technischen Bereichen versucht man heute diesen Lotus-Effekt nachzuempfinden: selbstreinigende Fassaden, Keramik und Fensterglas sind Beispiele für solch technische Entwicklungen. Unverzichtbar ist bei der Entwicklung solcher Produkte die Kontaktwinkelmessung.

Kontaktwinkelmessungen sind die Basis vieler Standards und Normen, welche Benetzungscharakteristiken beschreiben. Eine umfangreiche Liste der Normen findet sich hier.

Anwendungsbeispiele für Kontaktwinkelmessungen

Die Messung des Kontaktwinkels bietet sich immer dann an, wenn Festkörper und Flüssigkeiten aufeinandertreffen und wenn Benetzungs- und Haftungseigenschaften kontrolliert oder verändert werden. Die Anwendungsfelder sind dementsprechend vielfältig. Wichtige Beispiele sind:

• Oberflächenbeschichtungen: Messung des Kontaktwinkels auf beschichteten Materialien, um die Qualität und Gleichmäßigkeit der Beschichtung zu bewerten.
• Lackier- und Druckindustrie: Bewertung der Benetzbarkeit von Farben, Lacken und Druckfarben auf verschiedenen Substraten.
• Textilindustrie: Ermittlung der Benetzbarkeit von Textilfasern, um die Qualität von Textilbehandlungen, wie Imprägnierung oder Entwässerung, zu überprüfen.
• Medizinische Geräte: Charakterisierung der Benetzbarkeit von medizinischen Implantaten, um deren biokompatibles Verhalten zu beurteilen.
• Lebensmittelindustrie: Bewertung der Benetzbarkeit von Verpackungsmaterialien, um die Bedruckbarkeit sicherzustellen und Lagereigenschaften zu verbessern
• Halbleiterindustrie: Kontrolle der Benetzbarkeit auf Oberflächen von Halbleiterchips und -substraten für die Herstellung von Mikrochips.
• Umweltwissenschaften:Messung des Kontaktwinkels auf Blattoberflächen von Pflanzen zur Untersuchung der Selbstreinigungseffekte und der Wasserverteilung.
• Nanotechnologie: Charakterisierung der Benetzbarkeit von Nanomaterialien und Nanopartikeln, um deren Eigenschaften in verschiedenen Anwendungen zu optimieren.
• Öl- und Gasindustrie: Beurteilung der Benetzbarkeit von Gesteinsoberflächen, um das Verhalten von Öl- und Gasreservoiren besser zu verstehen.
• Reinigungs- und Entfettungsprozesse: Bewertung der Effizienz von Reinigungs- und Entfettungsmitteln auf verschiedenen Oberflächen, um die Wirksamkeit zu optimieren.